Home > Filters for the daily mean sea level computation

Filters for the daily mean sea level computation

Sea level observations are traditionally recorded as hourly heights. Subsequently, the mean sea level is derived using a linear combination of these heights (Bessero, 1985).

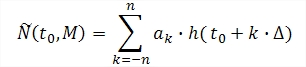
Fig. 1 : Mean sea level computation formulae, where M=2n+1,
∆ is the sampling, ak is a sequence of real coefficients.


Several such linear filters exist to compute the daily mean sea levels. Theoretically, the longer is the vector ak, the more efficient is the filter for the reduction of the tidal effects (it takes into account more observations), but the more limited will be its application in the case of tide gauge observations containing gaps. The Demerliac filter is a good trade-off recommended by the French hydrographic agency (SHOM). It uses a 71 elements symmetric vector ak (see the table below)

k Avergae of 25 heights
25*ak		Doodson filter
30*ak		Munk "Tide Killer" filter
10^7*ak		Godin filter
14400*ak		Demerliac filter
24576*ak
0 1 0 395287 444 768
1 1 2 386839 443 766
2 1 1 370094 440 762
3 1 1 354118 435 752
4 1 2 338603 428 738
5 1 0 325633 419 726
6 1 1 314959 408 704
7 1 1 300054 395 678
8 1 0 278167 380 658
9 1 2 251492 363 624
10 1 0 234033 344 586
11 1 1 219260 323 558
12 1 1 208050 300 512
13 0 195518 276 465
14 1 180727 253 435
15 0 165525 231 392
16 0 146225 210 351
17 1 122665 190 325
18 0 101603 171 288
19 1 85349 153 253
20 72261 136 231
21 60772 120 200
22 47028 105 171
23 30073 91 153
24 13307 78 128
25 66 105
26 55 91
27 45 72
28 36 55
29 28 45
30 21 32
31 15 21
32 10 15
33 6 8
34 3 3
35 1 1

Tab. 1 : Coefficients used for different linear filters. For each filter, ak=a-k.
Source : Bessero (1985)



Some useful links:
– R Script of the Demerliac filter
– R script of the Doodson filter
– R software website
[//]

References:
Bessero G. (1985). Marées. SHOM, Fascicule 2, chap. IX à XV.