_Home (hidden)
DOI ULR6a solution
– General information Access the data by clicking on the Download tab
Title: GPS Solution ULR6a
DOI identifier: 10.26166/sonel_ulr6a
Publisher: SONEL Data Center
Publication year: 2016
Version: a
Temporal coverage: 1995-01-01 / 2014-12-31
Language: English
– Creators
Alvaro Santamaria-Gomez [1], Médéric Gravelle [2], Guy Wöppelmann [2]
Affiliation: [1] GET, Observatoire Midi-Pyrénées/CNRS/IRD/UPS, Toulouse, France.
[2] LIENSs, CNRS/ULR, La Rochelle, France.
– Keywords
GPS, tide gauge, vertical land movements
– Contributors
LIENSs, La Rochelle, France
IGN, Saint Mandé, France
CNRS, France
La Rochelle Université, La Rochelle, France
– Data use information
Citation: A. Santamaria-Gomez, M. Gravelle, G. Wöppelmann (2016): GPS Solution ULR6. SONEL Data Center. doi: 10.26166/sonel_ulr6a.
Use rights: The ULR6a solution is freely available to anyone. It is asked to all users to acknowledge the SONEL Data Centre in their research papers.
– Description
The ULR6a solution has taken part to the second reprocessing campaign of the International GNSS Service (IGS). It corresponds to 749 stations for which the entire dataset between 1995.0 and 2013.9 was reprocessed using the most up-to-date models and corrections available at that time.
First, daily solutions are computed through the adjustment of positions of the global network of stations, Earth Orientation parameters, satellite orbits and zenith tropospheric delays. This process results in global daily solutions that are expressed in their own (daily) terrestrial frame.
Then, the daily times series are obtained after the combination of these daily solutions. The velocities are estimated simultaneously of the mean station position, station position offsets and transformation parameters (translation, rotation and scale) for the alignment to a unique terrestrial reference frame (ITRF08). A minimum of three continuous years without an offset (e.g., due to an equipment change or an earthquake) in the time series were required to estimate a “robust” vertical velocity, leading to a fields of 498 vertical velocities, among which 322 are nearby a tide gauge (<15 km).
The formal uncertainty of the estimated velocities has been computed taking into account the time-correlated noise in the residual time series to make them as realistic as possible. The median uncertainty on the estimated vertical velocities is about 0.36 mm/year.
– Related identifiers
SONEL URL: http://www.sonel.org/
– Acknowlegments
This solution has been proceeded thanks to the data provided by the Data Providers who collaborate with SONEL.
Calculating the mean sea levels
Definition and calculation of the mean sea levels
Mean sea level is a vague notion that needs to be clearly defined to have a good understanding of the signals contained in the series of values and to interpret the variations (temporal mean? spatial mean? in what extension?).
The definition adopted in SONEL corresponds to the definition of the Permanent Service for Mean Sea Level, the PSMSL, and of the Global Sea Level Observing System GLOSS to which SONEL contributes. The means are temporal averages at the tide gauges (point on the coast), over daily, monthly and annual periods.
There are, however, different ways to calculate these means. They are briefly summarised below:
– Annual values: arithmetic means of monthly means weighted for the number of days actually observed during the month. The value is calculated if at least 11 monthly values are actually available (cf. rules of the PSMSL).
– Monthly values : arithmetic means of daily means. However, the value is not calculated if more than 15 days are missing (cf. rules of the PSMSL).
– Daily values: the choice of an arithmetic mean over a 24h period has the disadvantage that it does not adequately filter the signals from periods of less than one day, particularly those from tides for which a period of 24h50 would be more suitable. Filters have been designed to do this (Doodson, Demerliac). Pugh (1987) reexamined the different filters and concluded that the differences were minimal for the monthly means at Newlyn (1-2 mm). We have adopted the Demerliac filter for historical reasons, but the Doodson filter is proposed to the users as well. Click on the link to find out more about filters.
File format
– The daily, monthly and annual heights are expressed in millimetres.
– The dates are in decimal years (centred on the 15th day of the month for monthly values and at midday for daily values).
Filters for the daily mean sea level computation
Sea level observations are traditionally recorded as hourly heights. Subsequently, the mean sea level is derived using a linear combination of these heights (Bessero, 1985).
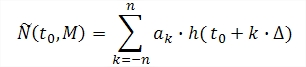
Fig. 1 : Mean sea level computation formulae, where M=2n+1,
∆ is the sampling, ak is a sequence of real coefficients.
Several such linear filters exist to compute the daily mean sea levels. Theoretically, the longer is the vector ak, the more efficient is the filter for the reduction of the tidal effects (it takes into account more observations), but the more limited will be its application in the case of tide gauge observations containing gaps. The Demerliac filter is a good trade-off recommended by the French hydrographic agency (SHOM). It uses a 71 elements symmetric vector ak (see the table below)
| k | Avergae of 25 heights 25*ak | Doodson filter 30*ak | Munk "Tide Killer" filter 10^7*ak | Godin filter 14400*ak | Demerliac filter 24576*ak |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 395287 | 444 | 768 |
| 1 | 1 | 2 | 386839 | 443 | 766 |
| 2 | 1 | 1 | 370094 | 440 | 762 |
| 3 | 1 | 1 | 354118 | 435 | 752 |
| 4 | 1 | 2 | 338603 | 428 | 738 |
| 5 | 1 | 0 | 325633 | 419 | 726 |
| 6 | 1 | 1 | 314959 | 408 | 704 |
| 7 | 1 | 1 | 300054 | 395 | 678 |
| 8 | 1 | 0 | 278167 | 380 | 658 |
| 9 | 1 | 2 | 251492 | 363 | 624 |
| 10 | 1 | 0 | 234033 | 344 | 586 |
| 11 | 1 | 1 | 219260 | 323 | 558 |
| 12 | 1 | 1 | 208050 | 300 | 512 |
| 13 | 0 | 195518 | 276 | 465 | |
| 14 | 1 | 180727 | 253 | 435 | |
| 15 | 0 | 165525 | 231 | 392 | |
| 16 | 0 | 146225 | 210 | 351 | |
| 17 | 1 | 122665 | 190 | 325 | |
| 18 | 0 | 101603 | 171 | 288 | |
| 19 | 1 | 85349 | 153 | 253 | |
| 20 | 72261 | 136 | 231 | ||
| 21 | 60772 | 120 | 200 | ||
| 22 | 47028 | 105 | 171 | ||
| 23 | 30073 | 91 | 153 | ||
| 24 | 13307 | 78 | 128 | ||
| 25 | 66 | 105 | |||
| 26 | 55 | 91 | |||
| 27 | 45 | 72 | |||
| 28 | 36 | 55 | |||
| 29 | 28 | 45 | |||
| 30 | 21 | 32 | |||
| 31 | 15 | 21 | |||
| 32 | 10 | 15 | |||
| 33 | 6 | 8 | |||
| 34 | 3 | 3 | |||
| 35 | 1 | 1 |
Tab. 1 : Coefficients used for different linear filters. For each filter, ak=a-k.
Source : Bessero (1985)
Some useful links:
– R Script of the Demerliac filter
– R script of the Doodson filter
– R software website
[//]
References:
Bessero G. (1985). Marées. SHOM, Fascicule 2, chap. IX à XV.
New station CGPS@TG
Help us to have the most complete and updated database
Other products
Sea and land levels at the coast
Welcome to SONEL
SONEL aims at providing high-quality continuous measurements of sea- and land levels at the coast from tide gauges (relative sea levels) and from modern geodetic techniques (vertical land motion and absolute sea levels) for studies on long-term sea level trends, but also the calibration of satellite altimeters, for instance.
SONEL serves as the GNSS data assembly centre for the Global Sea Level Observing System (GLOSS), which is developed under the auspices of the IOC/Unesco. It works closely with the PSMSL and the University of Hawaii Sea Level Center (UHSLC) by developing an integrated global observing system, which is linking both the tide gauge and the GNSS databases for a comprehensive service to the scientific community. It also acts as the interface with the scientific community for the French tide gauge data.